Back Propagation
梯度下降
梯度下降(gradient descent)在机器学习中应用十分的广泛,不论是在线性回归还是Logistic回归中,它的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。
思想
梯度下降法的基本思想可以类比为一个下山的过程。
假设这样一个场景:一个人被困在山上,需要从山上下来(找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低;因此,下山的路径就无法确定,必须利用自己周围的信息一步一步地找到下山的路。这个时候,便可利用梯度下降算法来帮助自己下山。怎么做呢,首先以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着下降方向走一步,然后又继续以当前位置为基准,再找最陡峭的地方,再走直到最后到达最低处;同理上山也是如此,只是这时候就变成梯度上升算法了。
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向。
数学表示
$$Θ^1=Θ^0+α▽J(Θ)→ evaluated at Θ^0$$
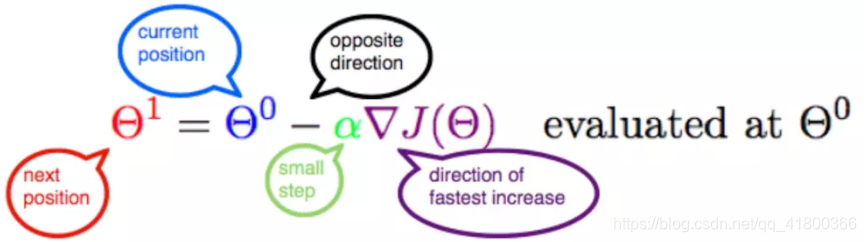
此公式的意义是:$J$是关于$Θ$的一个函数,我们当前所处的位置为$Θ^0$点,要从这个点走到J的最小值点,也就是山底。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是$α$,走完这个段步长,就到达了$Θ^1$这个点!
α
α 在梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离,**其实就是不要走太快,错过了最低点。同时也要保证不要走的太慢,导致太阳下山了,还没有走到山下。** 所以α的选择在梯度下降法中往往是很重要的!α不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点!
梯度要乘以一个负号
梯度前加一个负号,就意味着朝着梯度相反的方向前进!我们在前文提到,梯度的方向实际就是函数在此点上升最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号;那么如果时上坡,也就是梯度上升算法,当然就不需要添加负号了。

第 $l$ 层的误差项可以通过第 $l + 1$ 层的误差项计算得到,这就是误差的反向传播(BackPropagation,BP)。反向传播算法的含义是:第 $l$ 层的一个神经元的误差项(或敏感性)是所有与该神经元相连的第 $l + 1$ 层的神经元的误差项的权重和.然后,再乘上该神经元激活函数的梯度